This page and guide will help you learn how to calculate return on investment (ROI). In addition to providing you with a free tool, we'll also walk you through the return on investment calculation and other essential investing concepts.
We'll also touch on the power of compounding interest and how you can use it to save money for important life events such as retirement and significant purchases. We'll also cover how to calculate ROI to help you tie all these concepts together, so let's get started.
What is Return on Investment (ROI)?
What is the ROI meaning, exactly?
It's a metric that measures the efficiency of an investment. It is calculated by taking the total return on investment and dividing it by the amount of money initially invested. ROI is most commonly used to measure the performance of financial instruments such as stocks and savings accounts. It is also popularly applied to business activities such as marketing, fundraising, and employee productivity.
The most common ROI formula for how to calculate rate of return on investment is as follows:
ROI = (Gains from Investment – Cost of Investment) / Cost of Investment
For example, if you invest $1,000 in a stock and it increases in value to $1,200, then your ROI would be ($1,200-$1,000)/1,000 = 0.2.
You can express ROI as a percentage by multiplying the ROI by 100. So in our example, the ROI would be 20%.
The ROI calculation is similar to how to derive the return on invested capital:
ROIC = (Net Income - Dividends) / (Total Assets - Non-Interest Bearing Current Liabilities)
Our investment calculator is a good start for incorporating the idea of ROI to understand the efficiency of your investments.

What is Compounding Interest?
Compounding interest is a powerful financial tool to grow savings or investments over time. It is the process of earning interest (or a return) on the interest already accumulated. This is different from simple interest, which does not include interest that has been earned in the calculation of future interest.
For example, if you put $100 into an account that pays 10% interest annually, the interest earned in the first year will be $10. If the interest compounds annually, you will earn $110 ($100 + $10) in the second year. The interest earned in the second year will be $11 x 10% = $1.10. In the third year, you will earn $12.10 ($11 + $1.10), and so on.
You can test more examples using our compound interest calculator.
Compound Interest Examples
Here are some further examples of compounding interest. Let's say you invest $10,000, which gives you 5% compounding returns over 20 years.
Here's how that future value will change when interest compounds across different timeframes. Note how an investor would benefit from compounding interest when it accrues monthly and especially daily, thus leading to a higher future value at the end of 20 years:
- Future value when interest compounds yearly: $26,532.98.
- Future value when interest compounds monthly: $27,126.40
- Future value when interest compounds daily: $27,180.96
To illustrate how powerful daily and monthly compounding interest can be, let's go with a more practical example.
If you try to grow an initial $10,000 investment to $50,000 in ten years at a 5% interest rate, this is how much you'd need to contribute each month when your returns compound daily, monthly and yearly:
- When interest compounds daily, you would need to contribute $215.59 per month.
- When interest compounds monthly, you need to contribute $215.93 per month.
- When interest compounds yearly, you need to contribute $311.50 per month.
How Do You Calculate ROI?
A = P(1 + r/n)^nt is a formula used to calculate compound interest over a given period. Here's how you can use it for calculating compound interest step by step.
Step 1: Understand the variables in the equation.
First, understand the equation variables for the return-on-investment calculation:
- A is the amount
- P is the principal or initial amount invested.
- r is the annual interest rate.
- n is the number of times interest compounds per year.
- t is the number of years the money stays invested.
Step 2: Convert the annual interest rate to a decimal.
To convert the annual interest rate to a decimal, divide the annual rate by 100. For example, if the annual rate is 5%, divide 5 by 100 to get 0.05.
Step 3: Calculate the compound interest rate.
The compound interest rate is calculated by adding 1 to the decimal form of the annual rate, then dividing the result by the number of times the interest compounds per year. For example, if the annual rate is 5% and the interest compounds quarterly, the compound interest rate would be (1 + 0.05/4).
Step 4: Calculate the total.
You can calculate the total by plugging these numbers into the A = P(1 + r/n)^nt formula.
For example, if:
- Principal: $1,000
- Annual rate: 5%
- Interest compounds: Quarterly
If the money stays invested for 10 years, the entire calculation would look like this.
A = P(1 + r/n)^nt
A = $1,000(1 + 0.05/4)^4*10
A = $1,000(1 + 0.0125)^40
A = $1,643.62
How Do You Interpret ROI Calculations?
All else being equal, a high ROI indicates a good return on an investment, while a low ROI indicates a poor return on an investment.
When interpreting ROI, consider the investment context, including the risk associated with the investment and the potential for future growth. For instance, stocks with smaller market capitalizations and share prices, such as penny stocks, may have more upside potential in the context of stock investing. However, the risk of losing some or all of your initial investment is far higher. You can apply the same logic to growth stocks, particularly those in the rapidly changing technology sector.
To get a real sense of how large or small a company's market capitalization is, you can plug in some numbers into our market cap calculator and see instant results.
You can also use our price-to-earnings (P/E) ratio calculator to see if a company's P/E is low or high.
Something to note here when comparing the efficiency of investments: Consider an equivalent amount of risk. For example, since stocks are generally riskier and more volatile than real estate, one would expect a higher ROI investing in the former than the latter.
Also, consider comparing the ROI against investing benchmarks such as the risk-free rate and the average long-term return of a stock index like the S&P 500. If an investment of equivalent risk is underperforming one of these appropriate benchmarks, it may also fail to be a suitable investment.
Finally, ROI also doesn't consider the time value of money, so consider the time the investment took to generate a return. Investments that take a long time to produce yields are less desirable than investments that produce yields in a short time because inflation reduces the purchasing power of money over time, opportunity costs, and increased downside risk of losing your initial investment.
Consider giving our inflation calculator a try to get a broad sense of how inflation may change the return from your investments.
Examples of ROI Calculations
Here are two ROI examples and calculations taken from the world of investing.
Let's say you invested $10,000 in a stock. After one year, the stock has increased in value by 10%, and you have received a return of $1,000. The ROI of the investment would be 10%, calculated as follows:
ROI = Return / Cost
ROI = $1,000 / $10,000
ROI = 10%
In this example, a return of 10% is considered a good investment return. You've earned a higher return than the initial cost of the investment.
We can see another example of ROI in the real estate market. Let's say you purchase a property for $200,000. After one year, the property value has increased 10% and is now worth $220,000. The ROI of the investment would be 5%, calculated as follows:
ROI = Return / Cost
ROI = $20,000 / $200,000
ROI = 5%
In this example, a 5% return is still a good return on the investment, as the investor has earned a higher return than the initial cost.
How to Use the Investment Calculator
This calculator is a valuable tool to help you make investment decisions. You can use it to calculate four fields on this page: the initial amount, target amount, contributions and time invested values.
The tool's output displays to the right of the input area and above the graph. The value of your calculated field is shown in the graph's title and will appear once you hit the blue "calculate" button. Below the title, a multi-line graph shows additional values of the investment's balance, principal and accrued interest.
The tool will compute the selected calculated field for you and take care of working out the compounded interest.
Follow the step-by-step instructions below to start using it.
Step 1: Select your calculation.
To start using the calculator, select which field you'd like to calculate using the dropdown box next to the "calculate" label. This is the most critical step of the process of how to calculate return on invested capital, which will determine the calculator fields available to you.
You can calculate the initial amount, target amount, contributions and time invested fields shown on the calculator.

Step 2: Complete the fields.
Next, fill out the rest of the fields in the calculator. Assuming we want to calculate the "initial amount" field, we'd start by declaring our "targeted amount" and then work our way down to the "contributions" field. Note that you can set contributions monthly or yearly.
Once you complete these steps, we'll move on to the "time invested" field. Using the dropdown box, you can select from months or years. Finally, choose your interest rate percentage and whether interest compounds monthly or yearly. Once you're ready to see the results, click the "calculate" button.
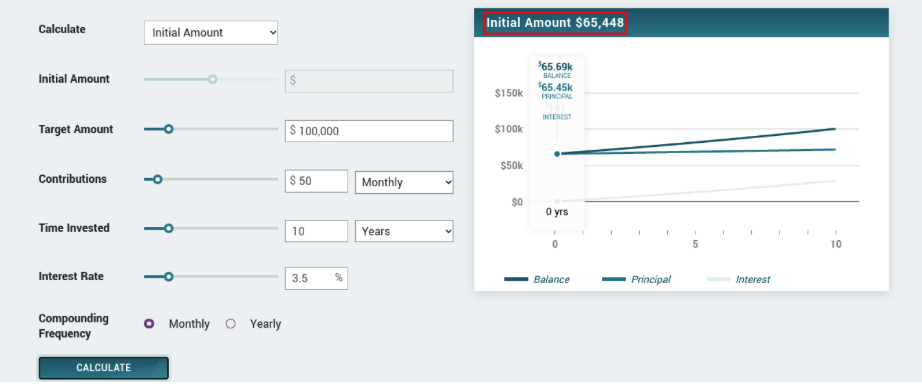
Step 3: Analyze your results.
Once you hit the "calculate" button, your calculation will appear in the graph's title, as seen in the example below. Other values for the investment's balance, principal, and interest will also appear as part of the multi-line chart.
Benefits of ROI
The benefits of ROI include the following:
- Greatest growth potential: ROI allows investors to identify stocks with the greatest growth potential.
- Ballpark gains: The formula assists in the decision-making process by indicating how much you can expect to gain in relation to the amount invested.
- Consistent returns: ROI calculations help create a portfolio of stocks with a higher likelihood of providing consistent returns.
- Compares performance: ROI calculations help compare the performance of different portfolio stocks and identify underperforming stocks.
- Helps determine timing: You can use it to determine the best time to enter or exit a stock position.
- Evaluate strategy: You can use it to evaluate the success of an existing stock strategy.
Limitations of ROI
On the other hand, consider some limitations of ROI:
- Time/value of money not considered: ROI does not consider the time/value of money, which is the idea that money invested today is worth more than money invested tomorrow.
- May not accurately reflect risk: ROI may not accurately reflect the risk associated with the investment.
- Cost of capital: ROI does not consider the cost of capital, which is the cost of borrowing money to invest.
- Liquidity: It does not consider the liquidity of the investment, which is an important factor for investors.
- Does not account for taxes: ROI does not account for taxes, which can significantly reduce the amount of money an investor receives.
- Opportunity cost not considered: It does not consider the opportunity cost of investing capital in one stock over another.
- Does not consider volatility: ROI does not consider the volatility of the market, which can affect the value of investments over time.
Alternatives to ROI
You can use several alternative methods to ROI to measure the success of an investment or project, including net present value (NPV), internal rate of return, payback period, cost-benefit analysis and economic value added.
- Net present value (NPV): NPV is a measure of the relative profitability of a project. It considers the project's cost, the expected future cash flows and the time value of money.
- Internal rate of return (IRR): IRR measures the return earned by an investment or project. It considers the project's cost, the expected future cash flows and the time value of money.
- Payback period: The payback period measures the time it takes for an investment or project to return its initial cost.
- Cost-benefit analysis: Cost-benefit analysis is a method used to assess a project's potential in terms of its benefits compared to cost.
- Economic value added (EVA): EVA measures a project's potential in terms of its ability to generate value for shareholders.
Variables Involved
Here’s an explanation of how the variables in the return on investment calculation can affect your total return.
Return Rate
The return rate is one of the key factors people should consider when determining the growth of an investment. All else being equal, a higher return rate will mean a higher final investment value. The return rate also helps determine the amount of time it takes for an investment to reach its desired amount, with a higher return rate shortening the length of time and a lower return rate extending the amount of time.
For example, it would take 67 years for an investor to grow a $10,000 investment to $100,000 assuming a 3.5% return rate that is compounded yearly with no additional contributions. By increasing the return rate to 4.5% and leaving other variables the same, it would take an investor just 53 years to reach $100,000, thus reducing the total investment horizon by 14 years.
Starting Amount
The starting amount is important as it will determine the total return when compounding. The more money you invest at the start, the more you will earn in interest, and the more you will benefit from the compounding effect.
For instance, investing a once-off amount of $20,000 that gives a return of 2.5% which compounds yearly will yield a total return of $25,601.59 in ten years. While investing a once-off amount of $30,000 will yield a total return of $38,402.52, all else being equal.
End Amount
The end amount or total return is the ultimate measure of an investment’s performance for a given period. It’s calculated by combining income from the investment like dividends or interest payments along with capital gains and losses that accrued during the period.
Investors might find the expected end amount useful by comparing certain investments against each other or against a standardized benchmark. Comparing a stock’s expected returns to investing in the S&P 500, for example, is a common way for people to know if they are beating the returns of the broader market.
Investment Length
Investment length gives the compounding effect more time to work its magic. The longer the time invested, the more the total return from the investment can increase. This means that investments with longer investment horizons can be more profitable than those with shorter ones, even if the initial investment and other variables are the same.
Illustrating this is that $10,000 invested over ten years with a return rate of 3.5% that compounds yearly will yield $14,105.99. While increasing the time invested to 15 years increases the total yield to $16,753.49.
Additional Contribution
Adding additional or ongoing contributions will increase an investor’s total return, all else being equal. Investing additional capital allows for greater amounts to be compounded over time by boosting its baseline principal amount.
Twenty thousand dollars invested over ten years with a return rate of 3.5% that compounds yearly with no additional contributions will yield $28,211.98. Investing just $500 a month over the investment period boosts the total return to $100,858.63, assuming all other variables are the same.
Types of Investments
Here’s a list of investment types you can invest in and apply the ROI principle.
Certificate of Deposit
A certificate of deposit (CD), sometimes known as a term deposit, is an investment instrument banks and credit unions commonly offer. These types of investments suit those with a low-risk profile, such as retirees, or to balance out an aggressive portfolio through (almost) guaranteed returns. CDs come with expiration or maturity dates.
Generally, the longer the maturity date, the higher the interest rate an investor receives, but the return is generally less than other investment instruments at an average of around 1.20% for the past five years. The issue with investing in CDs is that their returns may not keep up with the rate of inflation, and they also tie up capital that could be used to yield higher gains elsewhere, thus incurring the holder a potentially steep opportunity cost.
Bonds
Bonds are the next step up in the risk ladder, offering investors potentially higher returns. Governments, institutions and other entities with various yields and grades of quality can issue bonds. All else being equal, the riskier the bond is to hold (judged by its credit rating), the higher its interest rate will be. A bond's return is measured by its coupon rate and commonly pays out monthly.
If you buy a $100,000 bond with a 5% coupon rate that has a 10-year maturity date, you will receive $5,000 per year for ten years. You will also receive your initial $100,000 investment back at the end of the 10 years. The issue with investing in bonds is similar to CDs, but their returns are also not guaranteed, especially when buying junk bonds or emerging market bonds in unstable economies, which can make them as risky as buying some types of stocks.
Stocks
Owning stocks, or shares, has provided historically strong returns over the past 10 years. The average return of the S&P 500, for example, is around 14% per year. That said, bear markets in equities do happen and can last around nine months on average. Although stocks have bounced back from previous bear markets, there is no guarantee that will continue to rise in the future.
Another issue is that stocks are generally more volatile than investments that have lower risk profiles, and this effect can be profound and difficult to recover from. For example, a $100,000 stock portfolio that loses 50% of its value will reduce to $50,000. For investors to get back to even, they will now need to yield a 100% gain to recoup their $50,000 loss, which may be beyond their investment horizon to realize.
Real Estate
Real estate is loved by many and can be a useful tool for diversifying an investment portfolio and reducing volatility. Due to population growth and demand for accommodation in general, house prices in the U.S. have grown around 5.5% yearly since the early 1990s. However, there are a few disadvantages of investing in physical property, such as incurring significant mortgage debt and paying hefty interest payments. Paying a large mortgage may be unsustainable for many families in a high-interest rate environment.
The other drawback is that it ties up large amounts of capital in a relatively illiquid asset that can't be converted into cash quickly. Investors seeking diversification into real estate may opt instead to buy shares in real estate investment trusts (REITs) that can more easily be bought and sold when the need arises while also benefiting from their often lucrative quarterly dividend payments.
Commodities
Commodities are some of the oldest investment instruments known to man, with a shining example being gold. The precious metal is a safe haven due to being universally valued with practical use in modern electronics. It has also seen a steady capital appreciation over the last few decades. The major downside to gold is that holding it doesn't yield dividends or gains outside of capital appreciation. It also soars in times of economic uncertainty but performs poorly when times are good.
Outside of investing in gold, commodities are generally affected by the forces of supply and demand more than anything else, which are unpredictable and difficult for investors to measure. Commodities may seem more volatile than stocks and can lead to wild swings that may cause you to chase losses to get back to even.
ROI: A Vital Concept for Investors
It's vital to recognize ROI and understand the broad strokes of its use. Although it may lack nuance, it is also invaluable for getting a high-level overview of the efficiency of an investment and its performance, all else being equal.